Research Highlights
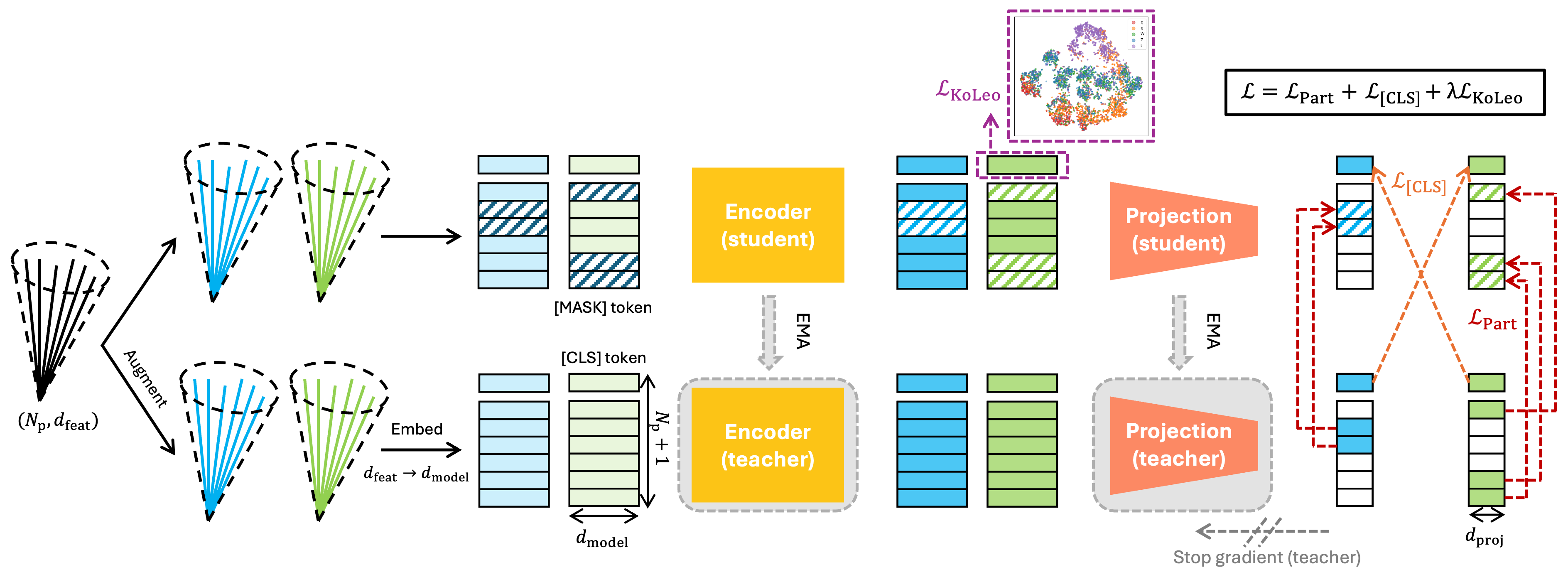
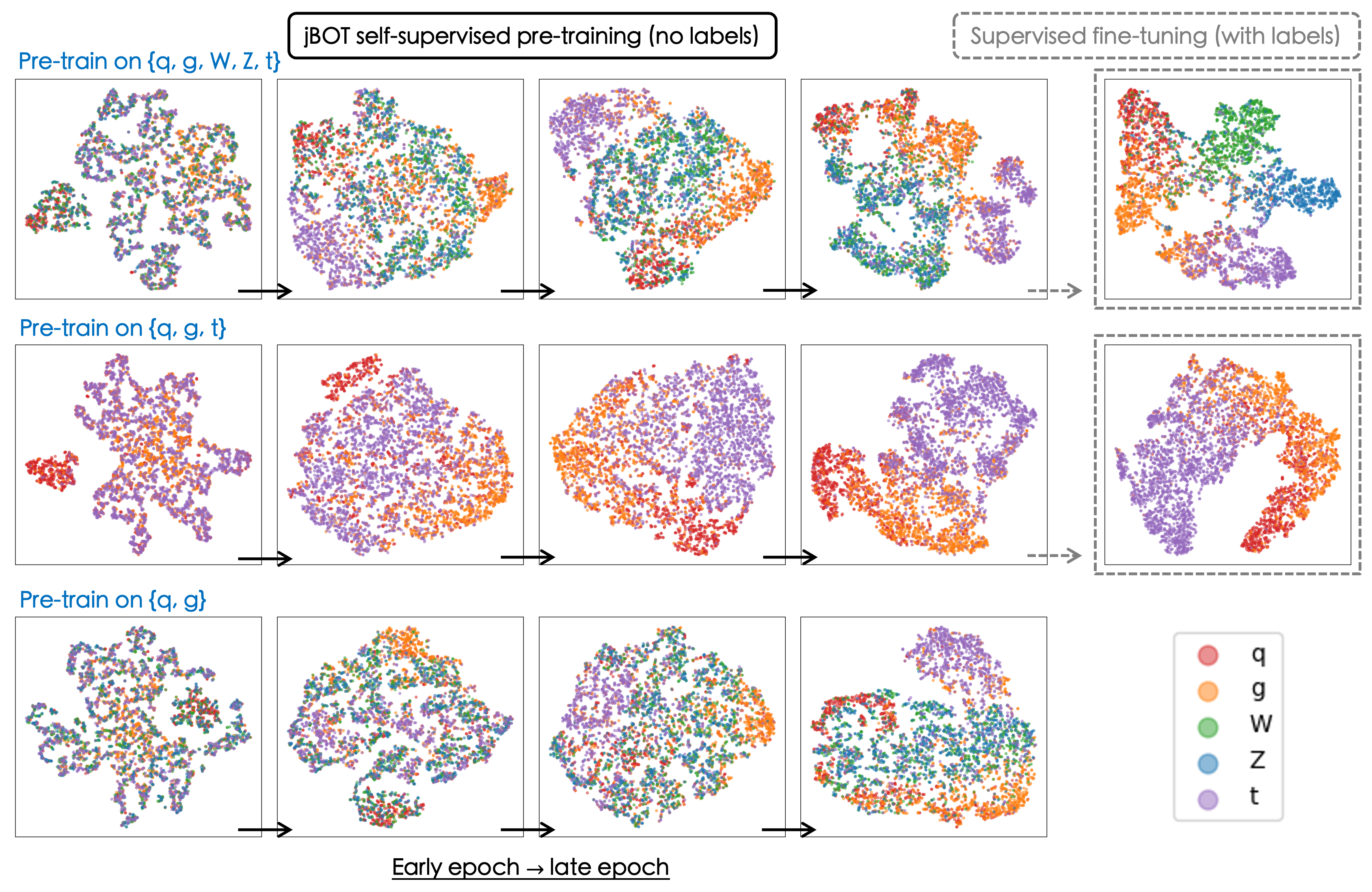
jBOT: Semantic Jet Representation Clustering Emerges from Self-Distillation
Self-supervised learning is a powerful pre-training method for learning feature representations without labels, which often capture generic underlying semantics from the data and can later be fine-tuned for downstream tasks. In this work, we introduce jBOT, a pre-training method based on self-distillation for jet data from the CERN Large Hadron Collider, which combines local particle-level distillation with global jet-level distillation to learn jet representations that support downstream tasks such as anomaly detection and classification. We observe that pre-training on unlabeled jets leads to emergent semantic class clustering in the representation space. The clustering in the frozen embedding, when pre-trained on background jets only, enables anomaly detection via simple distance-based metrics, and the learned embedding can be fine-tuned for classification with improved performance compared to supervised models trained from scratch.
Paper: arXiv:2601.11719 Code: https://github.com/hftsoi/jbot
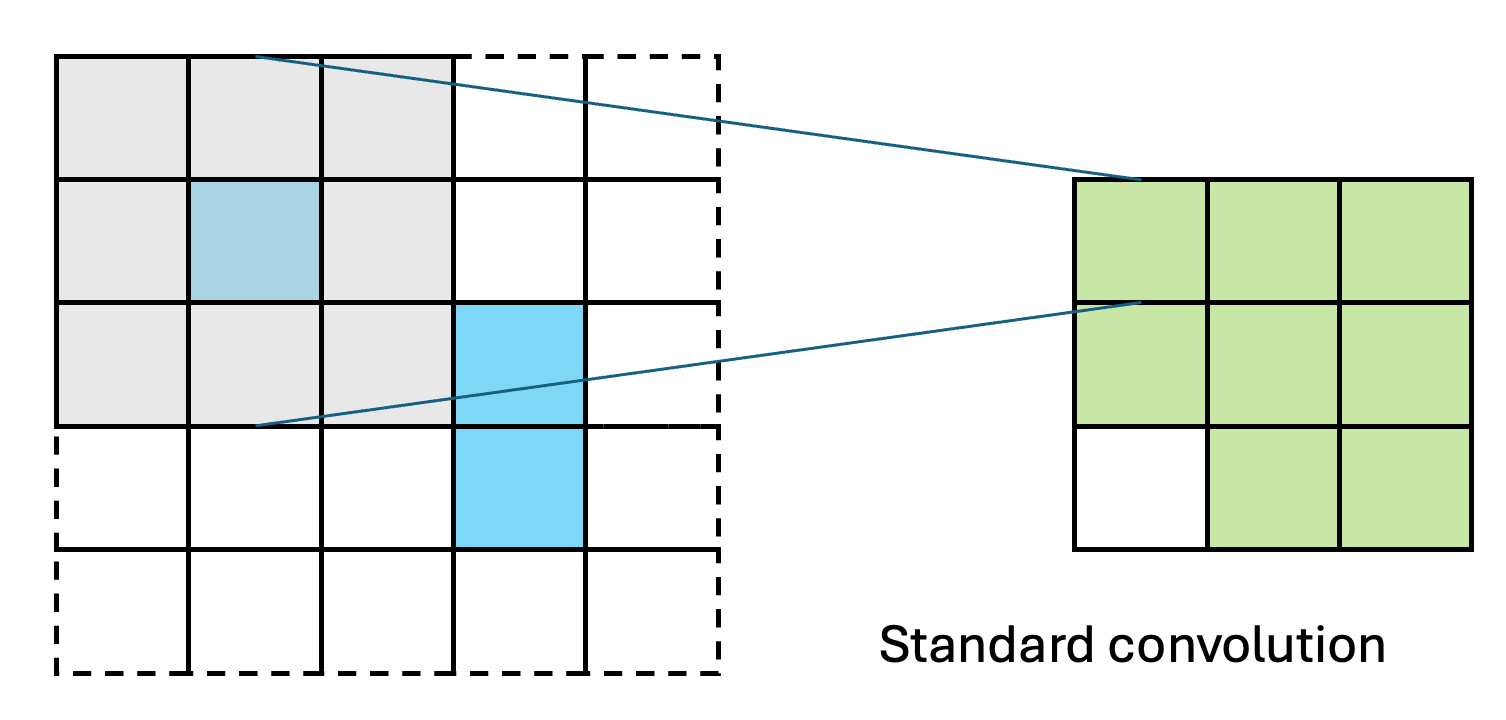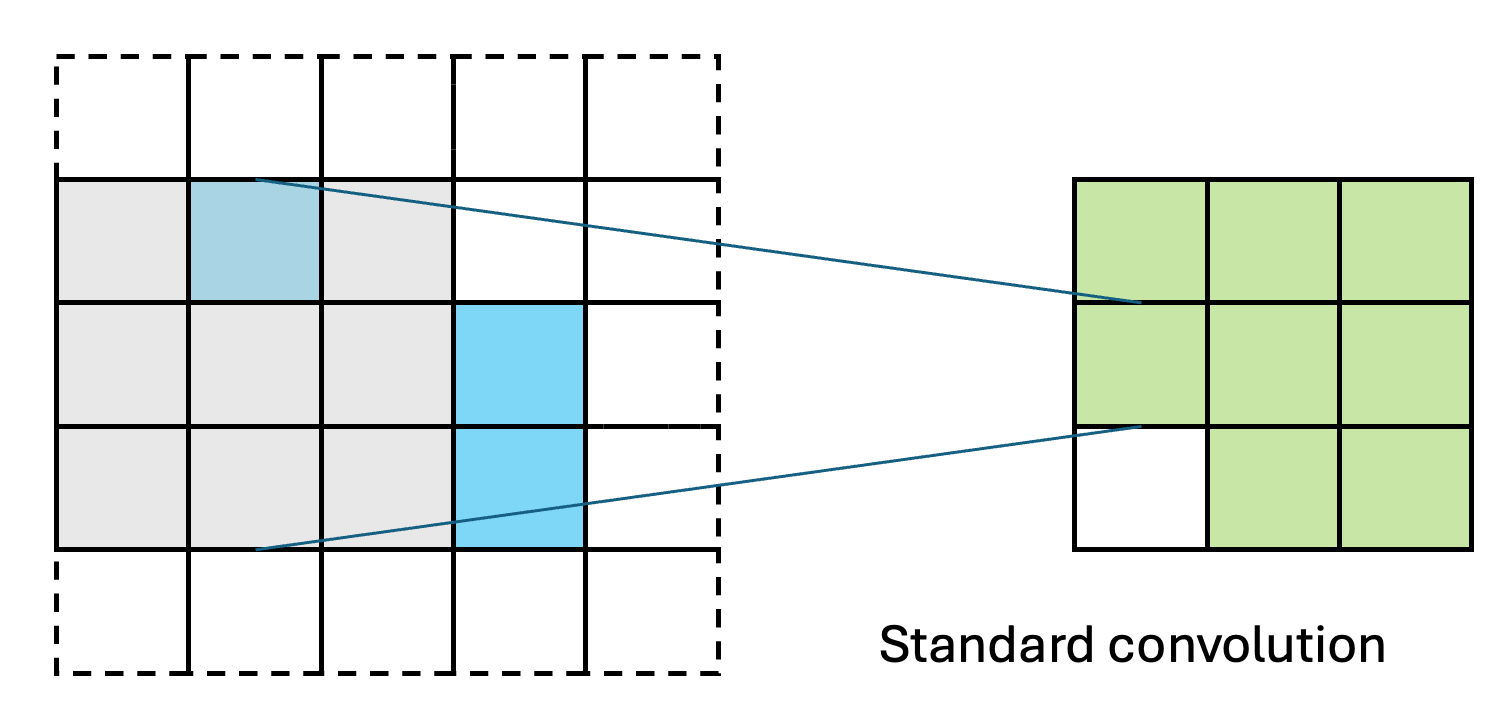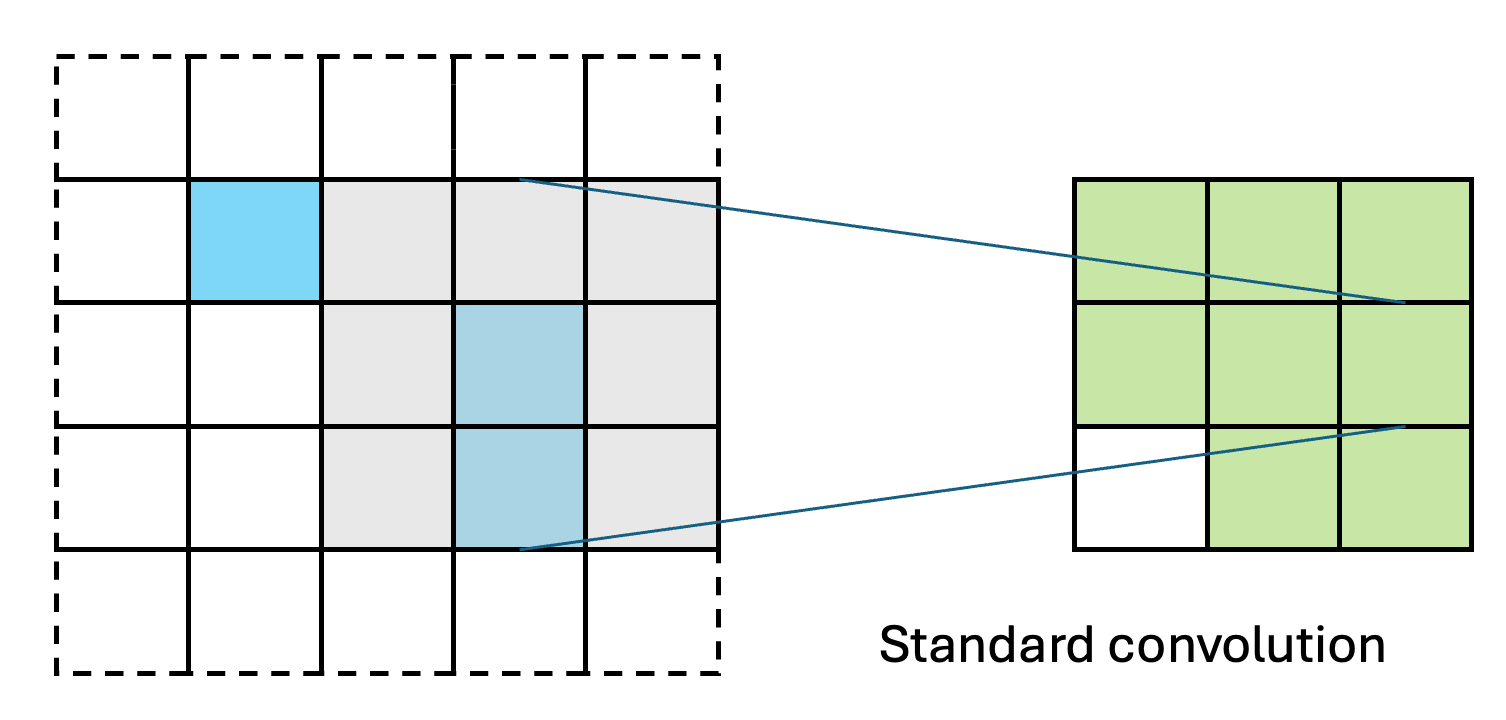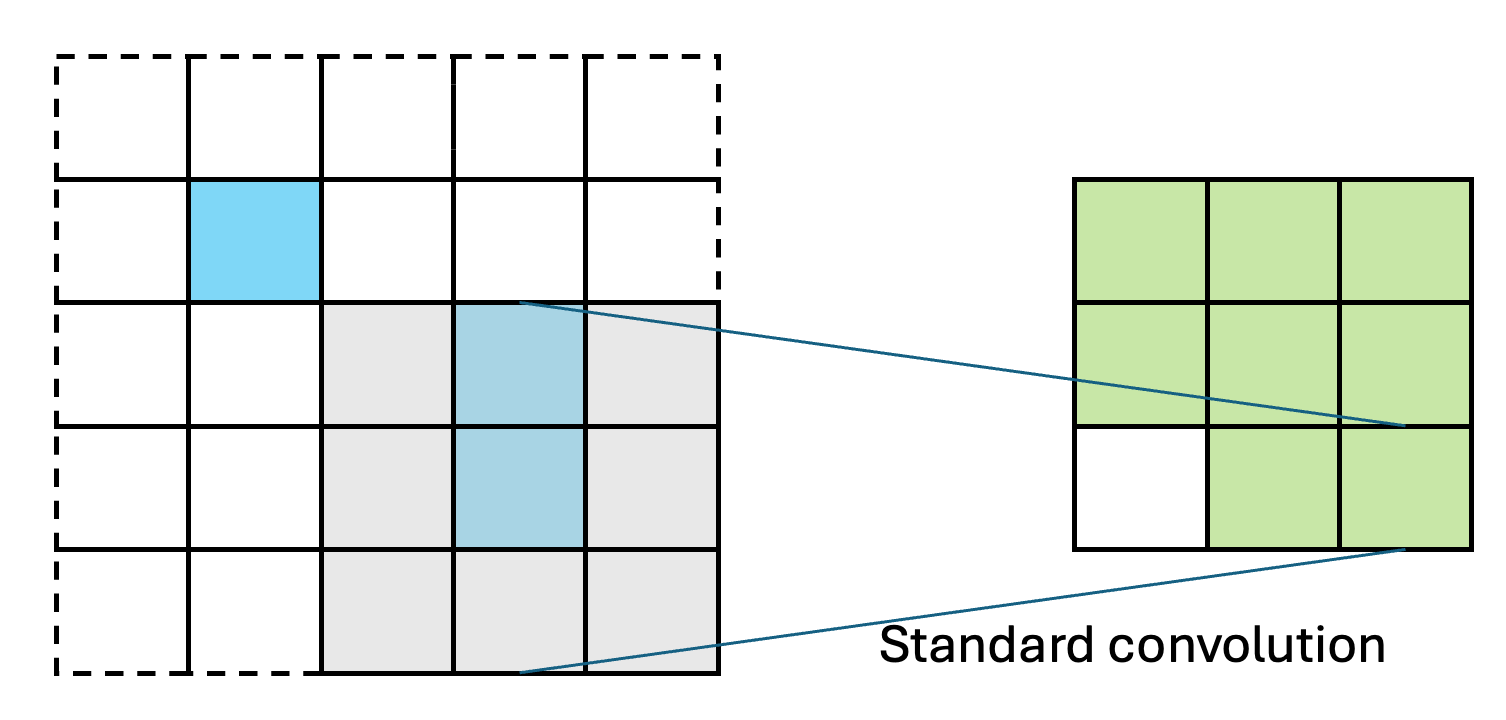
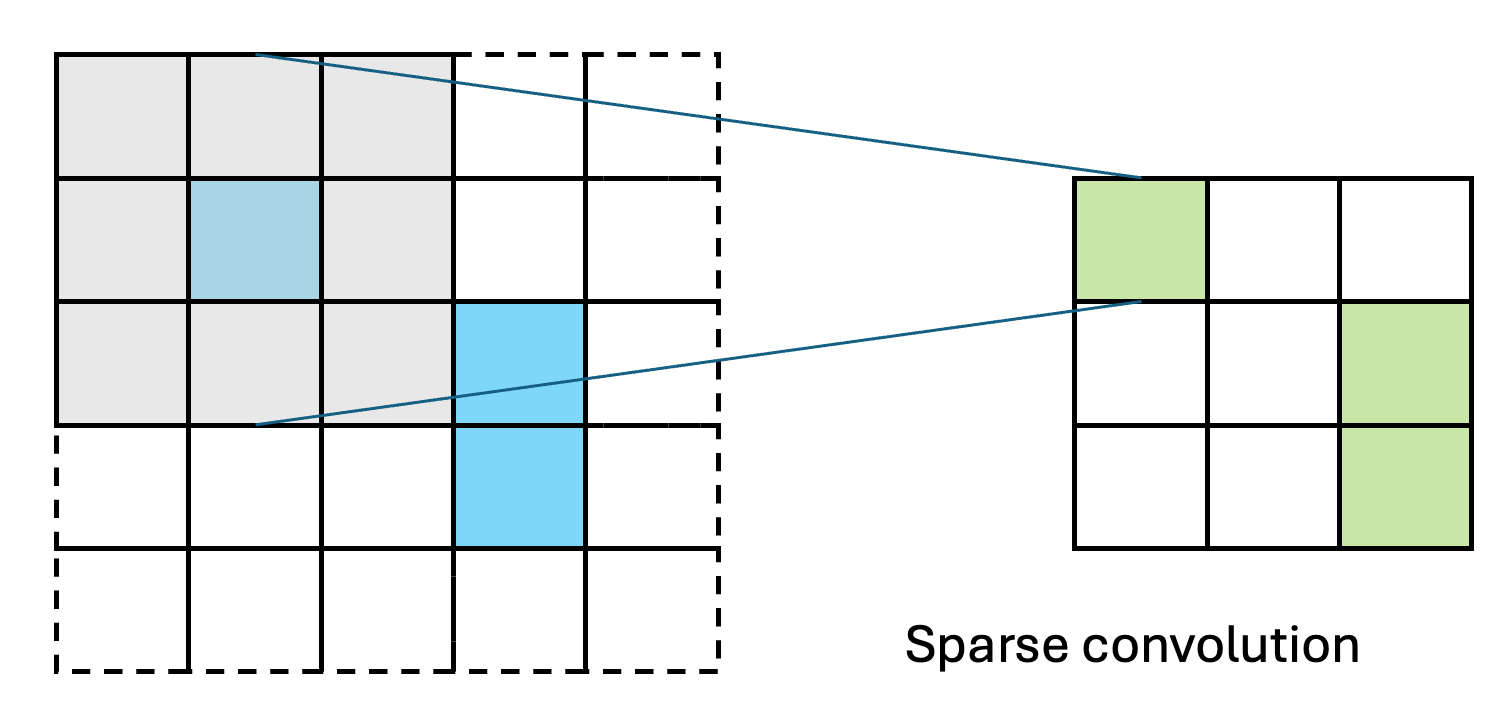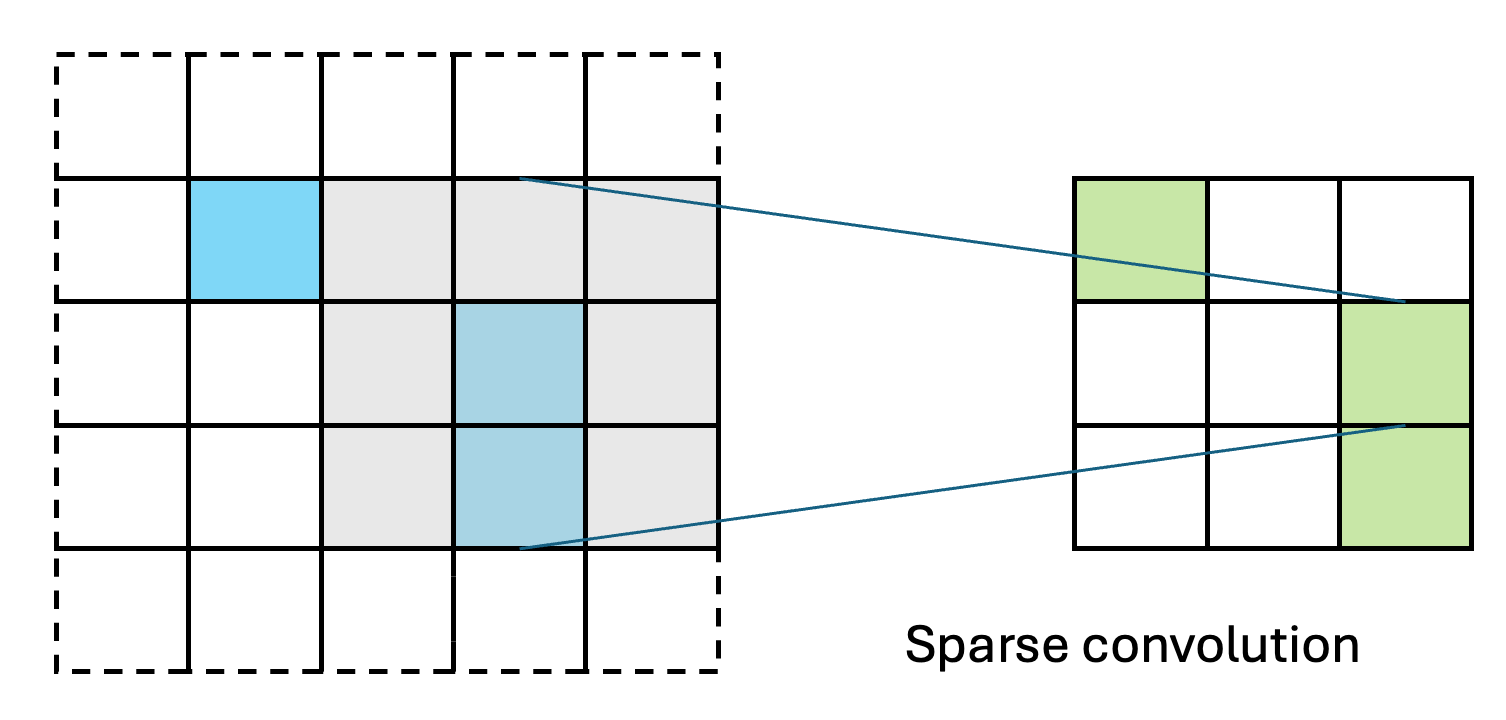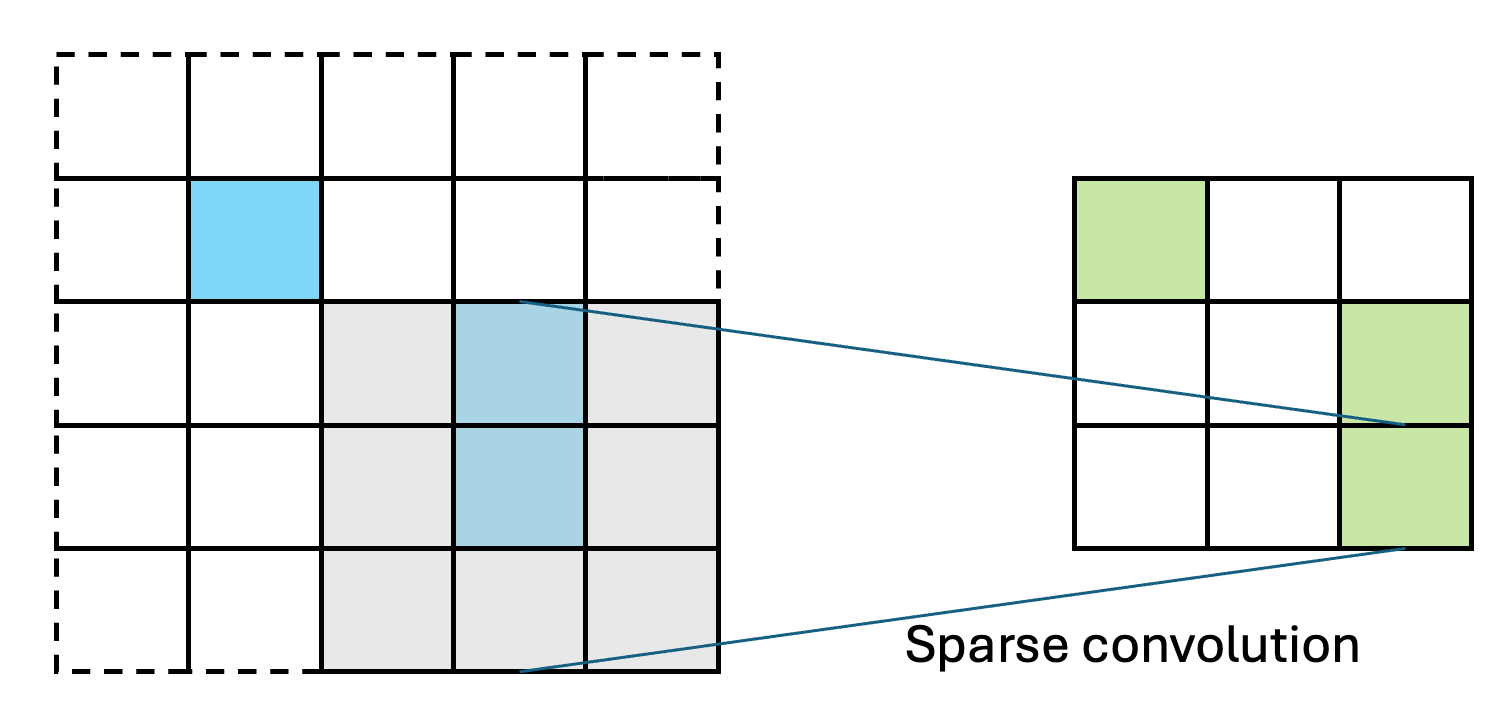
SparsePixels: Efficient Convolution for Sparse Data on FPGAs
Inference of standard convolutional neural networks (CNNs) on FPGAs often incurs high latency and a long initiation interval due to the deep nested loops required to densely convolve every input pixel regardless of its feature value. However, input features can be spatially sparse in some image data, where semantic information may occupy only a small fraction of the pixels and most computation would be wasted on empty regions. In this work, we introduce SparsePixels, a framework that implements sparse convolution on FPGAs by selectively retaining and computing on a small subset of active pixels while ignoring the rest. We show that, for identifying neutrino interactions in naturally sparse LArTPC images with 4k pixels, a standard CNN with a compact size of 4k parameters incurs an inference latency of 48.665 \(\mu\)s on an FPGA, whereas a sparse CNN of the same base architecture, computing on less than 1% of the input pixels, achieves a \(\times\)73 speedup to 0.665 \(\mu\)s with resource utilization well within on-chip budgets, trading only a small percent-level performance loss. This work aims to benefit future algorithm development for efficient data readout in modern experiments with latency requirements of microseconds or below.
Paper: arXiv:2512.06208 Code: https://github.com/hftsoi/sparse-pixels
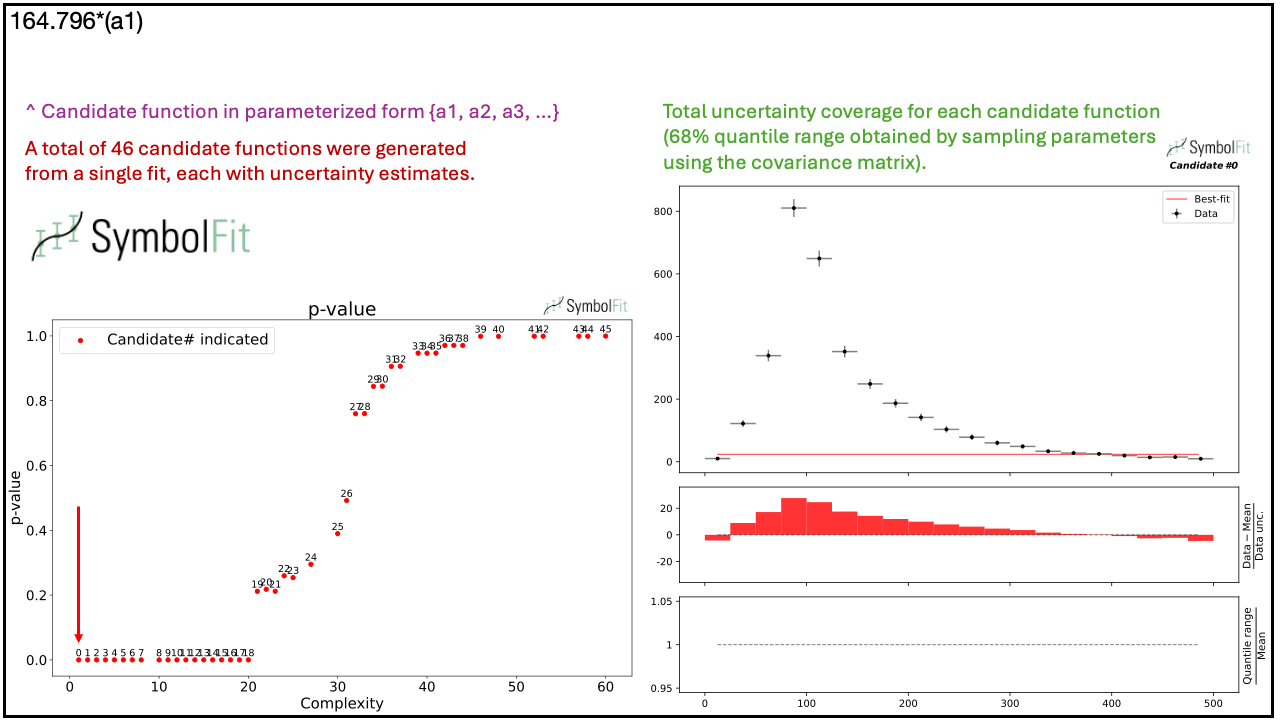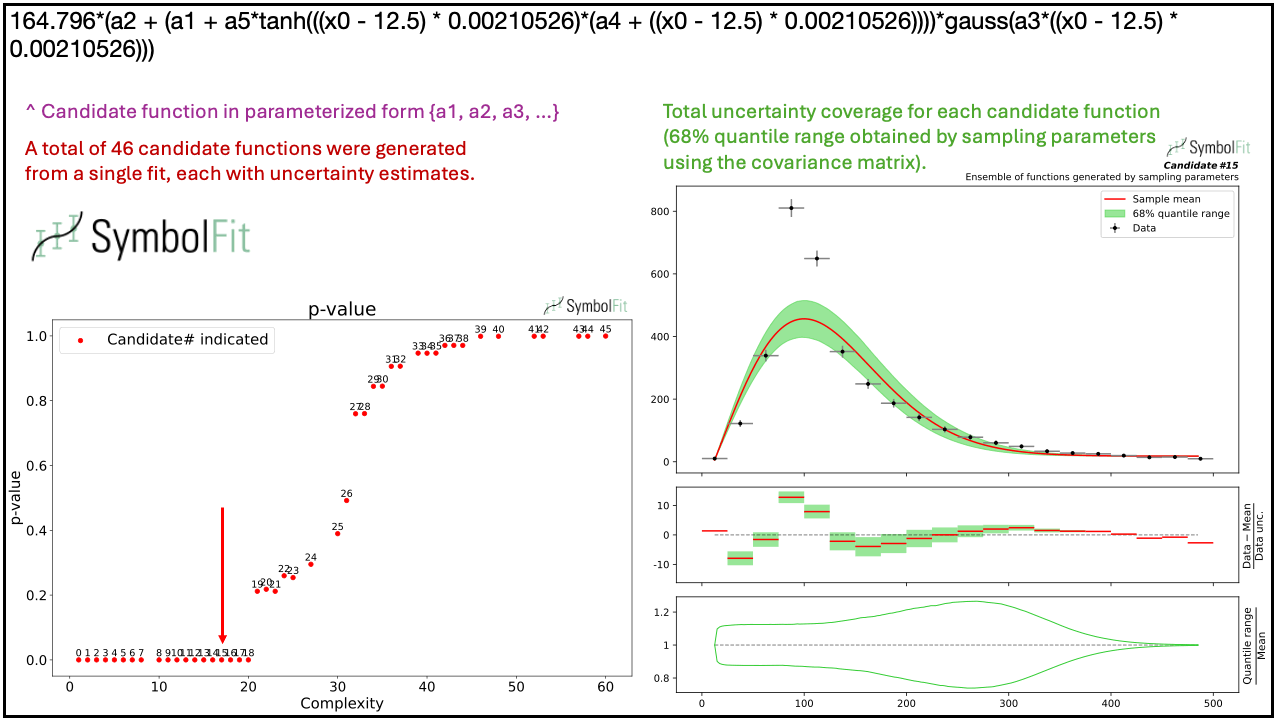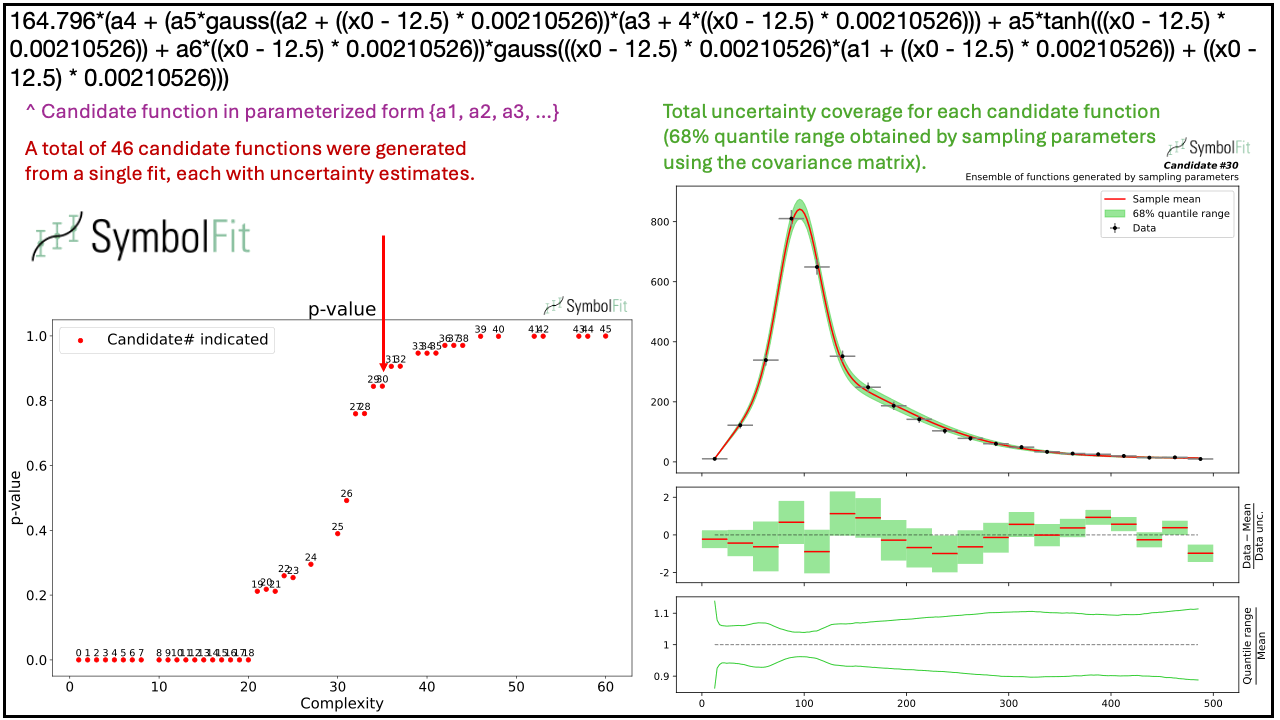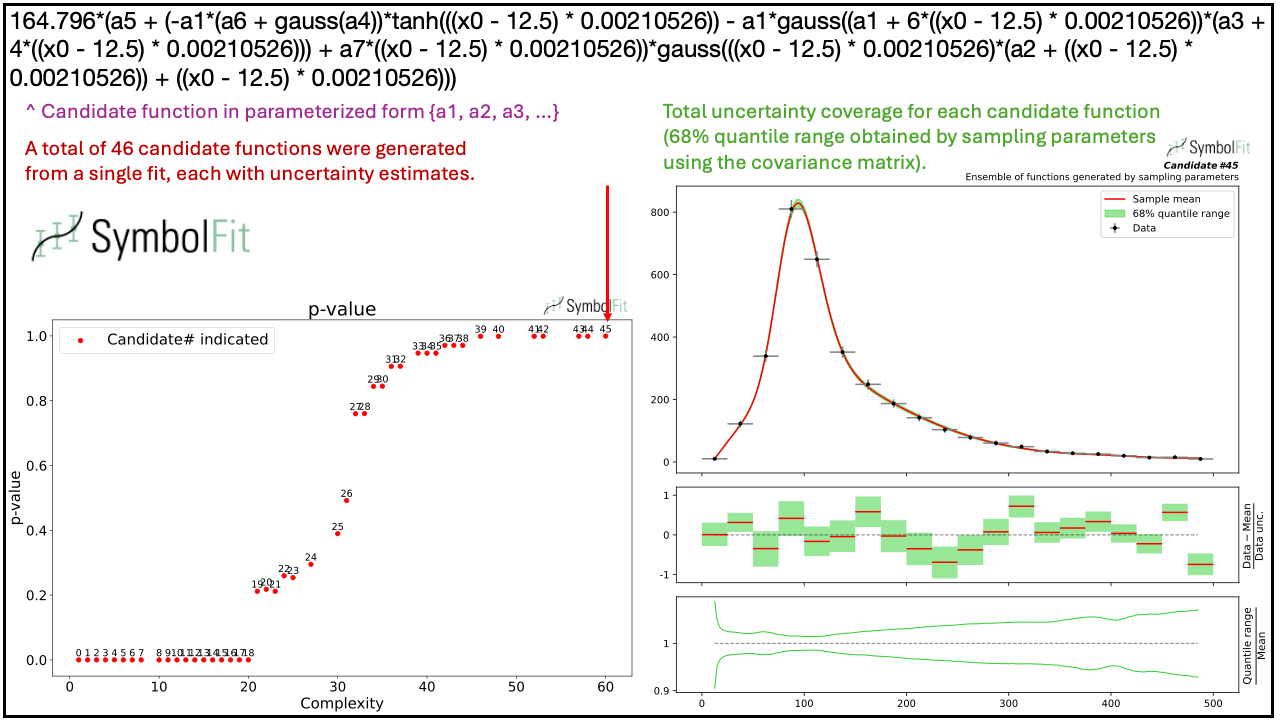
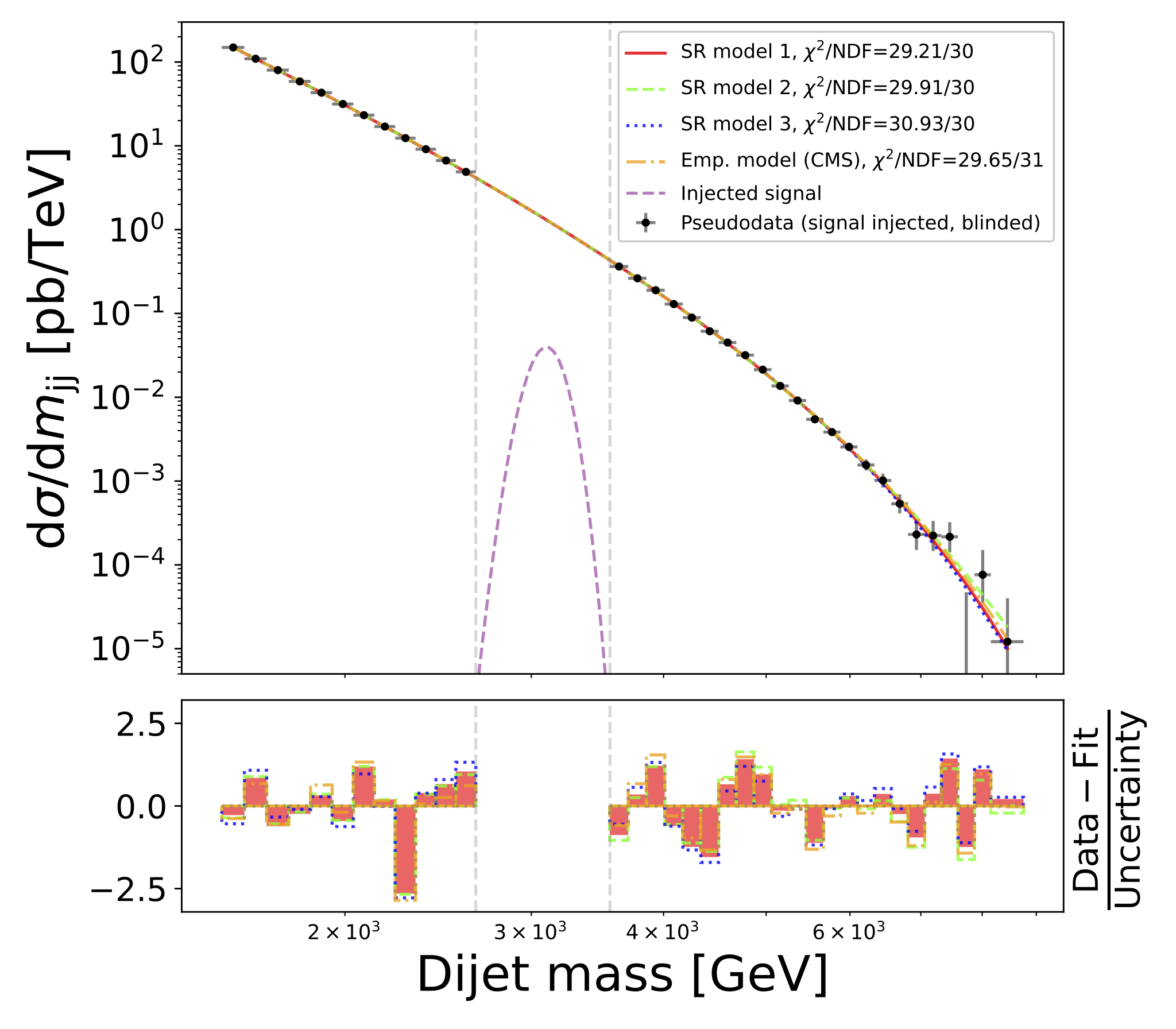
SymbolFit: Automatic Parametric Modeling with Symbolic Regression
We introduce SymbolFit, a framework that automates parametric modeling by using symbolic regression to perform a machine-search for functions that fit the data while simultaneously providing uncertainty estimates in a single run. Traditionally, constructing a parametric model to accurately describe binned data has been a manual and iterative process, requiring an adequate functional form to be determined before the fit can be performed. The main challenge arises when the appropriate functional forms cannot be derived from first principles, especially when there is no underlying true closed-form function for the distribution. In this work, we develop a framework that automates and streamlines the process by utilizing symbolic regression, a machine learning technique that explores a vast space of candidate functions without requiring a predefined functional form because the functional form itself is treated as a trainable parameter, making the process far more efficient and effortless than traditional regression methods. We demonstrate the framework in high-energy physics experiments at the CERN Large Hadron Collider (LHC) using five real proton-proton collision datasets from new physics searches, including background modeling in resonance searches for high-mass dijet, trijet, paired-dijet, diphoton, and dimuon events. We show that our framework can flexibly and efficiently generate a wide range of candidate functions that fit a nontrivial distribution well using a simple fit configuration that varies only by random seed, and that the same fit configuration, which defines a vast function space, can also be applied to distributions of different shapes, whereas achieving a comparable result with traditional methods would have required extensive manual effort.
Paper: arXiv:2411.09851 Code: https://github.com/hftsoi/symbolfit

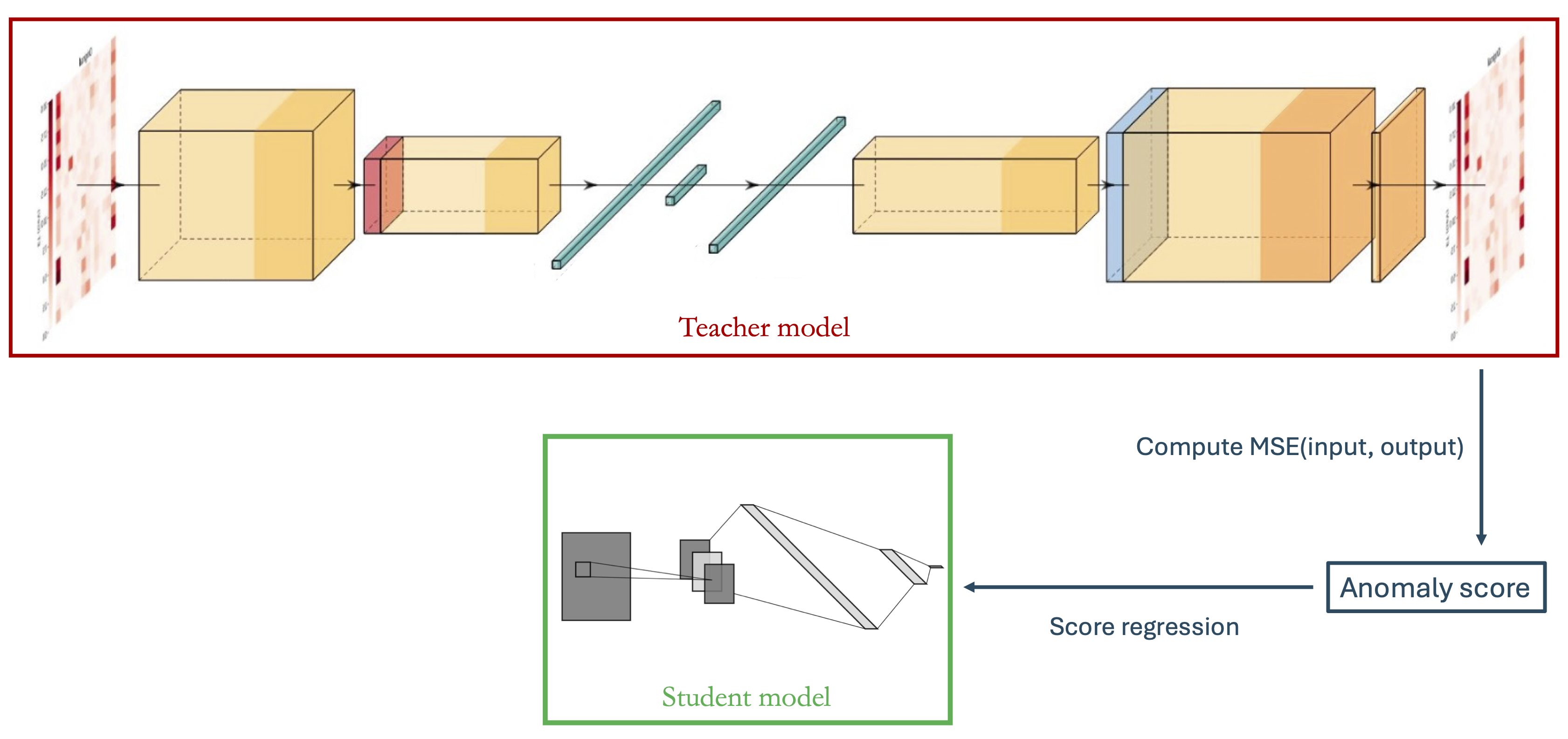
CICADA: Anomaly Detection for New Physics Searches at the CMS Level-1 Trigger
BSM physics has yet to be discovered at the LHC. Three possibilities remain: new physics cannot be produced given the current center-of-mass energy, more data need to be collected, or the physics may be present but we are looking in the wrong places and making the wrong event selections. The first round of event selection at CMS occurs at the Level-1 trigger, and machine learning (ML) can be used to search for new physics while minimizing human bias. CICADA (Calorimeter Image Convolutional Anomaly Detection Algorithm) is a novel ML-based trigger algorithm that uses anomaly detection technique to search for new physics in a model-agnostic way as close to the raw collision data as possible, i.e. the CMS Level-1 trigger. The model is an autoencoder that takes the low-level calorimeter energy deposits at the trigger-tower level as inputs and is trained unsupervisedly on the raw collision data to learn input reconstruction. This allows the model to detect a wide range of rare SM and BSM processes as anomalies whenever they are differently distributed from the majority of the collision data, namely the soft QCD processes. CICADA is developed and ready for the Run 3 deployment and will serve as a baseline for the preparation for the HL-LHC.
CMS Detector Performance Summaries: CERN-CMS-DP-2023-086 Home: CICADA
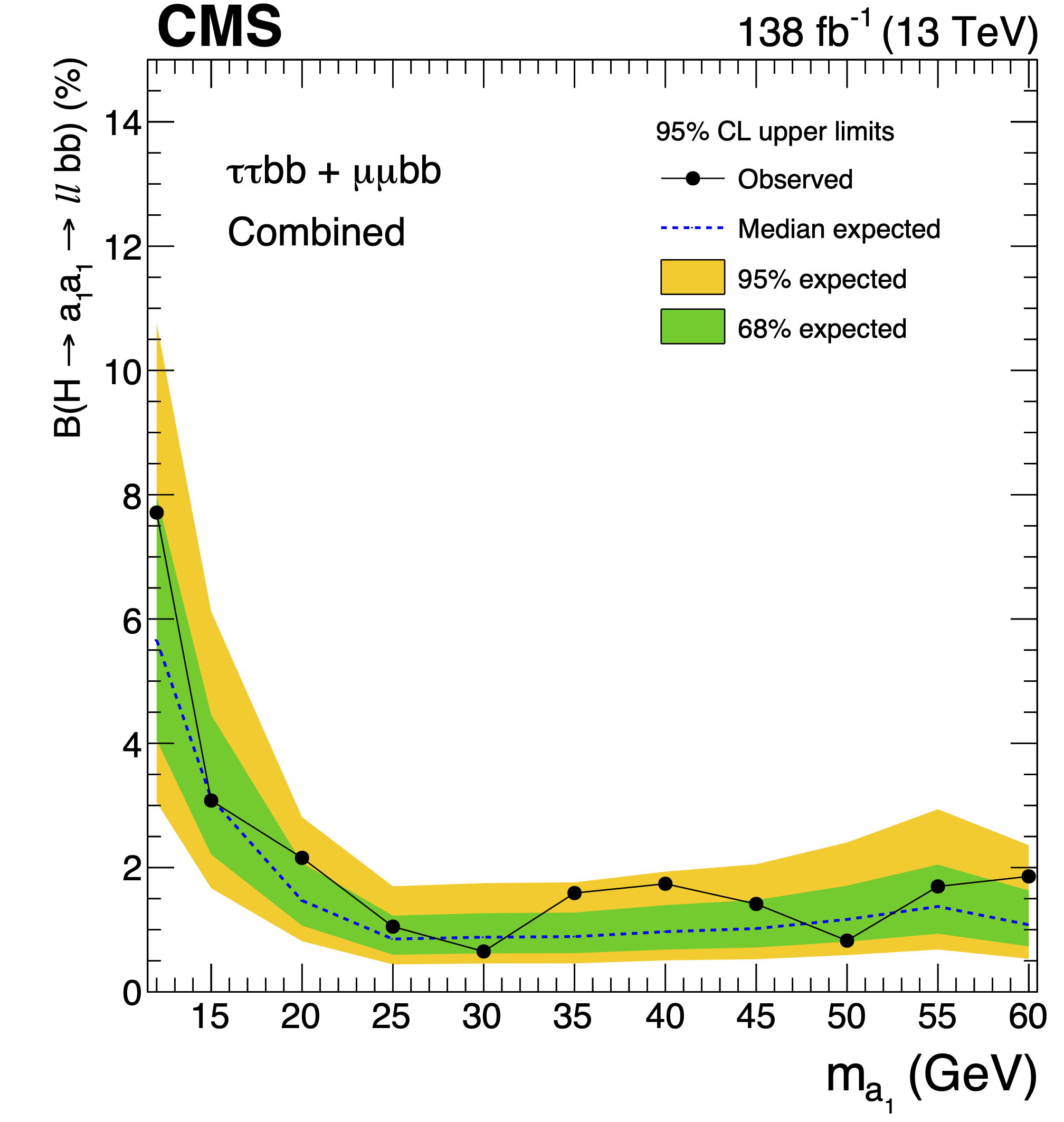
Search for exotic decays of the Higgs boson to a pair of pseudoscalars in the \(\mu\mu\)bb and \(\tau\tau\)bb final states
A search for exotic decays of the Higgs boson (H) with a mass of 125 GeV to a pair of light pseudoscalars \(\text{a}_{1}\) is performed in final states where one pseudoscalar decays to two b quarks and the other to a pair of muons or \(\tau\) leptons. A data sample of proton-proton collisions at \(\sqrt{s} = 13\) TeV corresponding to an integrated luminosity of 138 \(\text{fb}^{−1}\) recorded with the CMS detector is analyzed. No statistically significant excess is observed over the standard model backgrounds. Upper limits are set at 95% confidence level (CL) on the Higgs boson branching fraction to μμbb and to \(\tau\tau\)bb, via a pair of \(\text{a}_{1}\)s. The limits depend on the pseudoscalar mass \(m_{\text{a}_{1}}\) and are observed to be in the range \((0.17-3.3) \times 10^{-4}\) and \((1.7-7.7) \times 10^{−2}\) in the \(\mu\mu\)bb and \(\tau\tau\)bb final states, respectively. In the framework of models with two Higgs doublets and a complex scalar singlet (2HDM+S), the results of the two final states are combined to determine model-independent upper limits on the branching fraction \(\mathcal{B}(H \rightarrow \text{a}_{1}\text{a}_{1} \rightarrow ll\text{bb})\) at 95% CL, with \(l\) being a muon or a \(\tau\) lepton. For different types of 2HDM+S, upper bounds on the branching fraction \(\mathcal{B}(H \rightarrow \text{a}_{1}\text{a}_{1})\) are extracted from the combination of the two channels. In most of the Type II 2HDM+S parameter space, \(\mathcal{B}(H \rightarrow \text{a}_{1}\text{a}_{1})\) values above 0.23 are excluded at 95% CL for \(m_{\text{a}_{1}}\) values between 15 and 60 GeV.
Paper: arXiv:2402.13358 HEPData: 10.17182/hepdata.145999
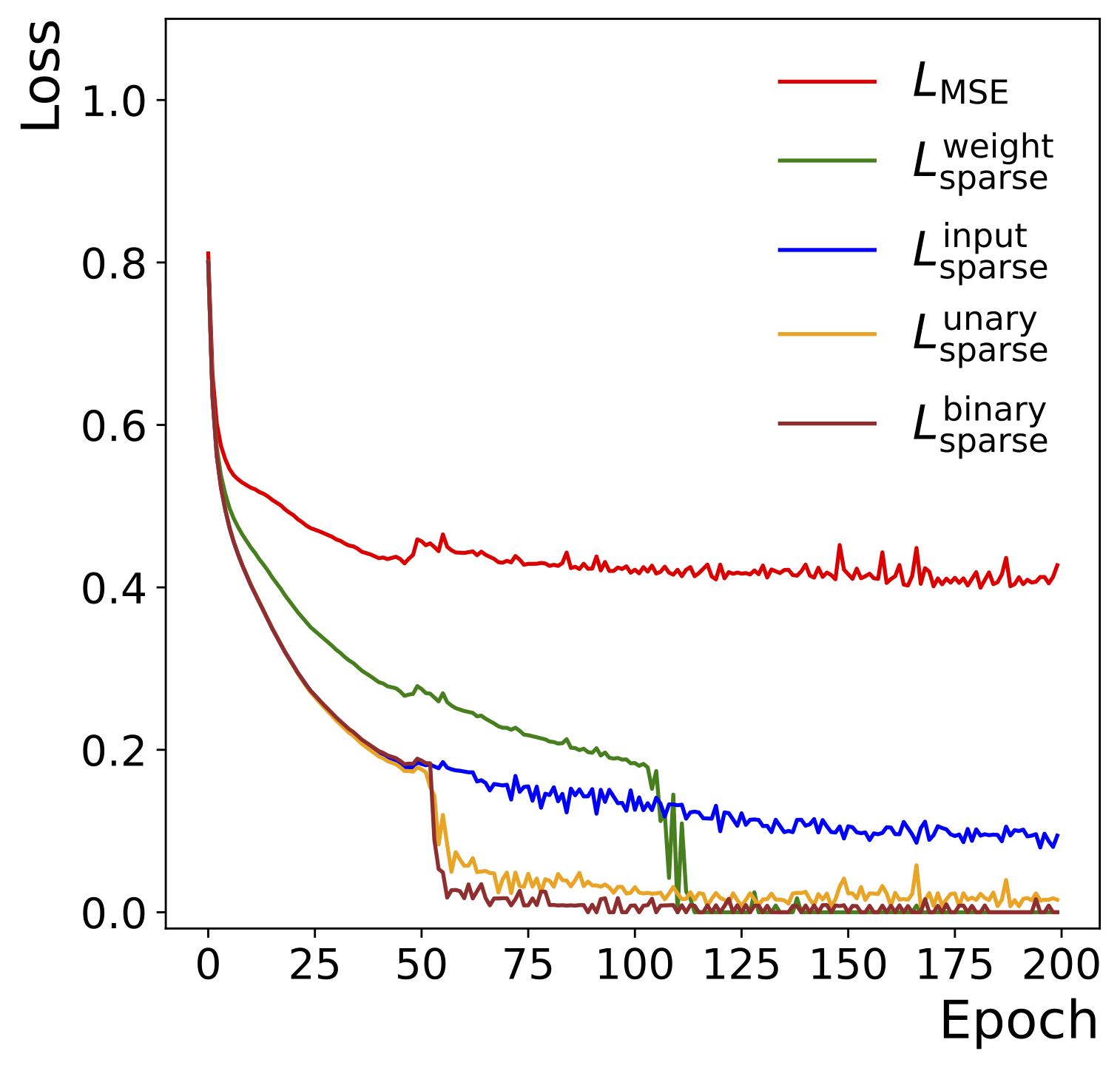
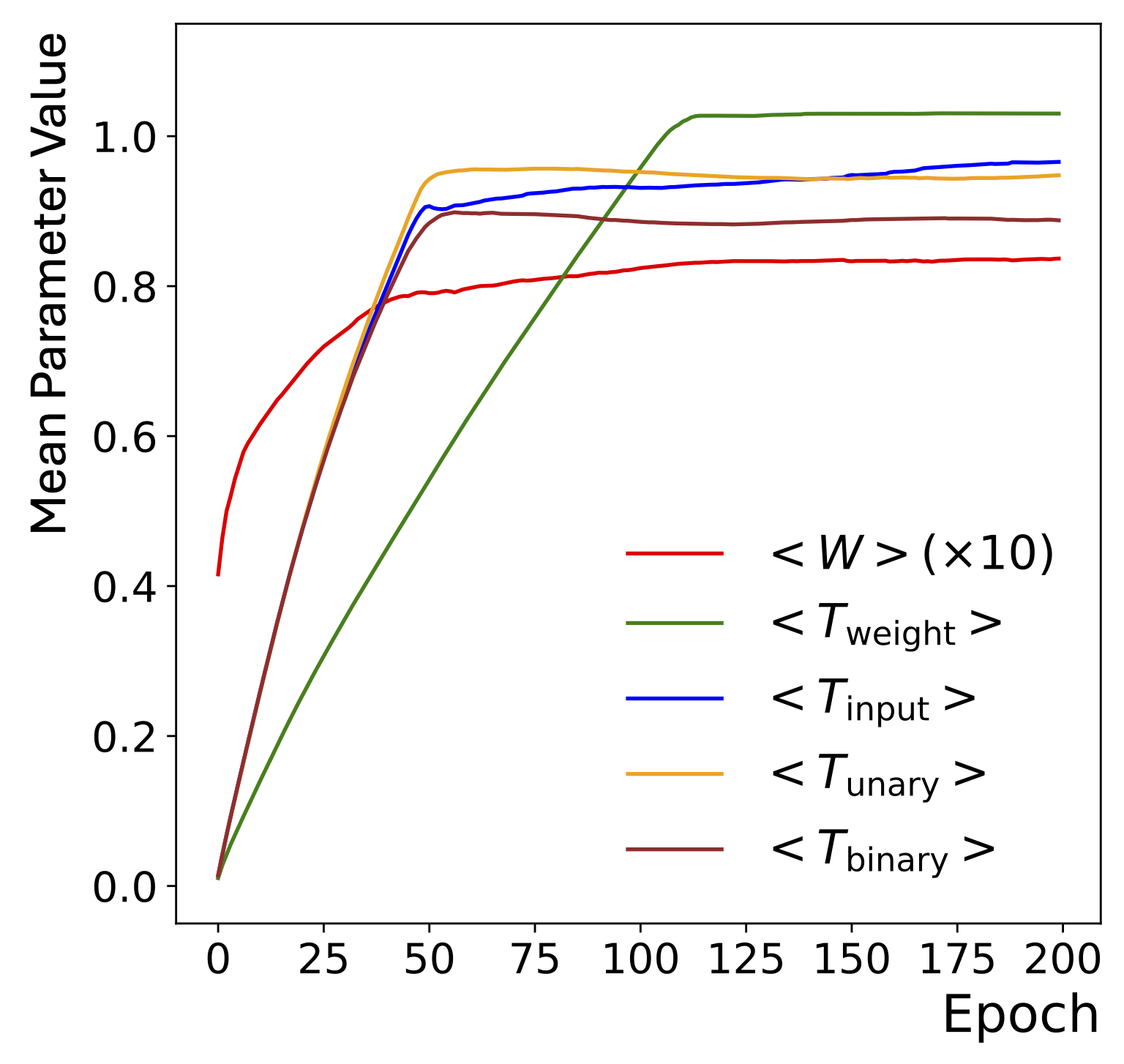
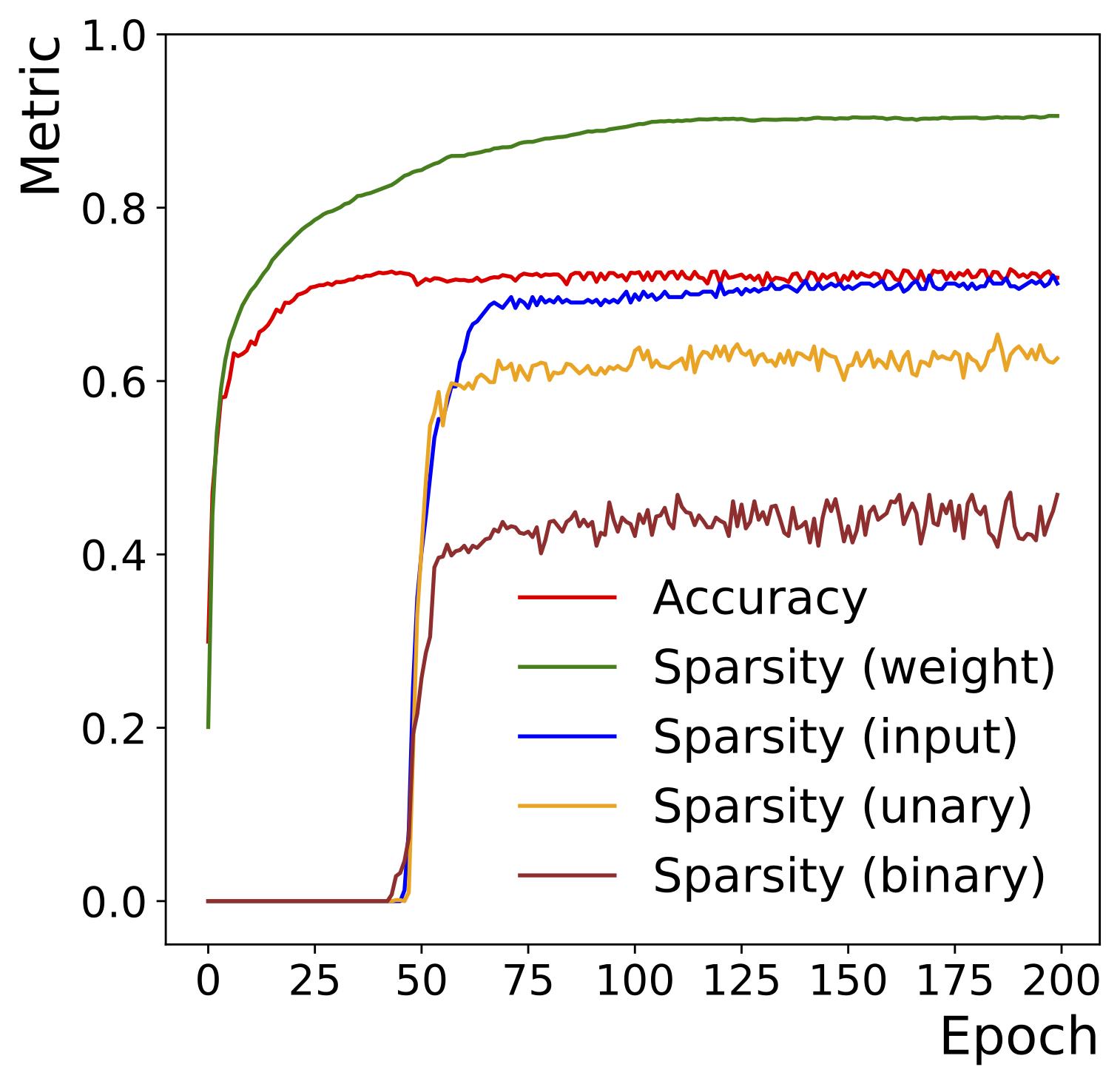
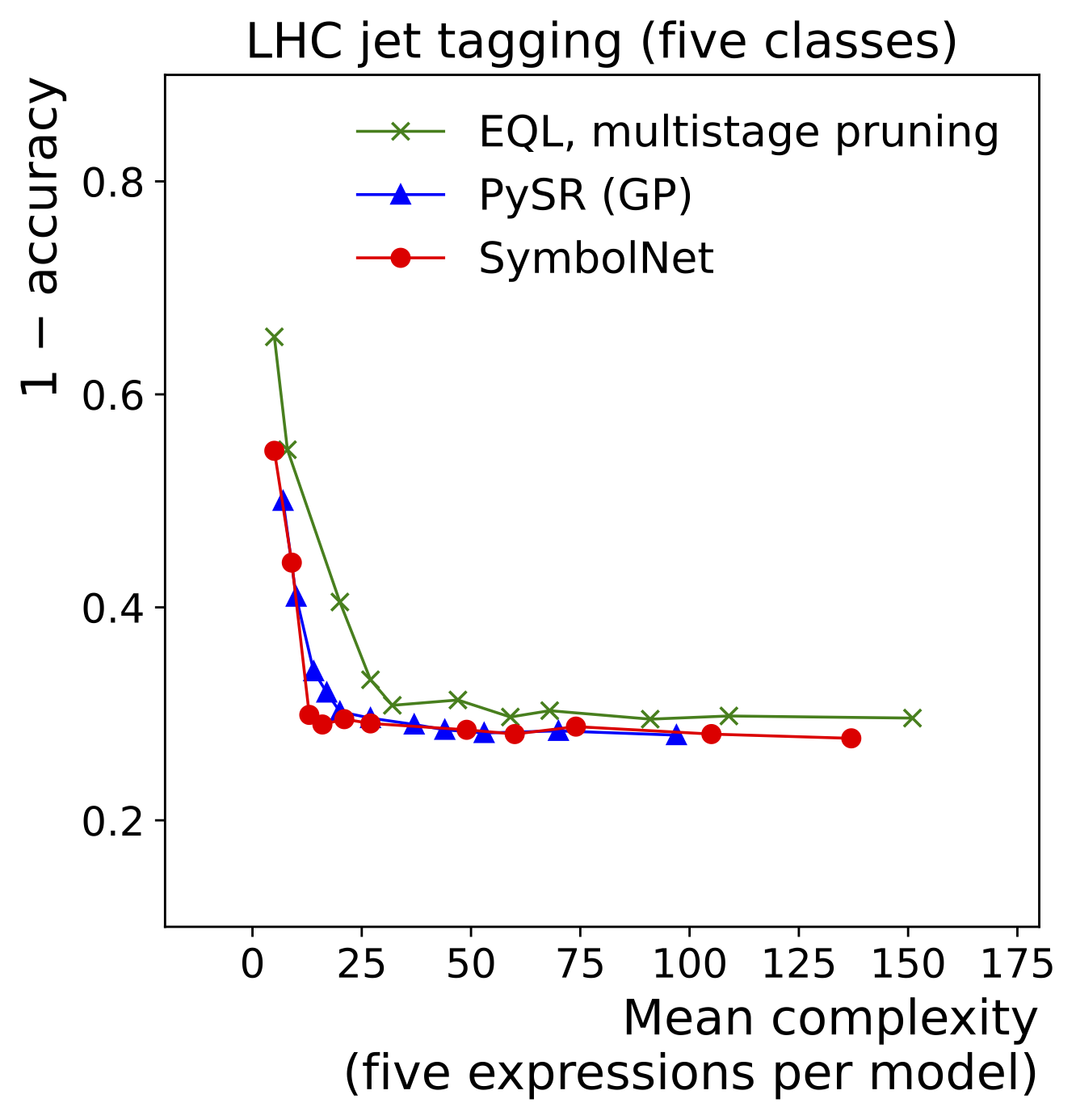
SymbolNet: Neural Symbolic Regression with Adaptive Dynamic Pruning for Compression
Compact symbolic expressions have been shown to be more efficient than neural network models in terms of resource consumption and inference speed when implemented on custom hardware such as FPGAs, while maintaining comparable accuracy. These capabilities are highly valuable in environments with stringent computational resource constraints, such as high-energy physics experiments at the CERN Large Hadron Collider. However, finding compact expressions for high-dimensional datasets remains challenging due to the inherent limitations of genetic programming, the search algorithm of most symbolic regression methods. Contrary to genetic programming, the neural network approach to symbolic regression offers scalability to high-dimensional inputs and leverages gradient methods for faster equation searching. Common ways of constraining expression complexity often involve multistage pruning with fine-tuning, which can result in significant performance loss. In this work, we propose SymbolNet, a neural network approach to symbolic regression specifically designed as a model compression technique, aimed at enabling low-latency inference for high-dimensional inputs on custom hardware such as FPGAs. This framework allows dynamic pruning of model weights, input features, and mathematical operators in a single training process, where both training loss and expression complexity are optimized simultaneously. We introduce a sparsity regularization term for each pruning type, which can adaptively adjust its strength, leading to convergence at a target sparsity ratio. Unlike most existing symbolic regression methods that struggle with datasets containing more than \(\mathcal{O}(10)\) inputs, we demonstrate the effectiveness of our model on the LHC jet tagging task (16 inputs), MNIST (784 inputs), and SVHN (3072 inputs).
Paper: arXiv:2401.09949 Code: https://github.com/hftsoi/SymbolNet
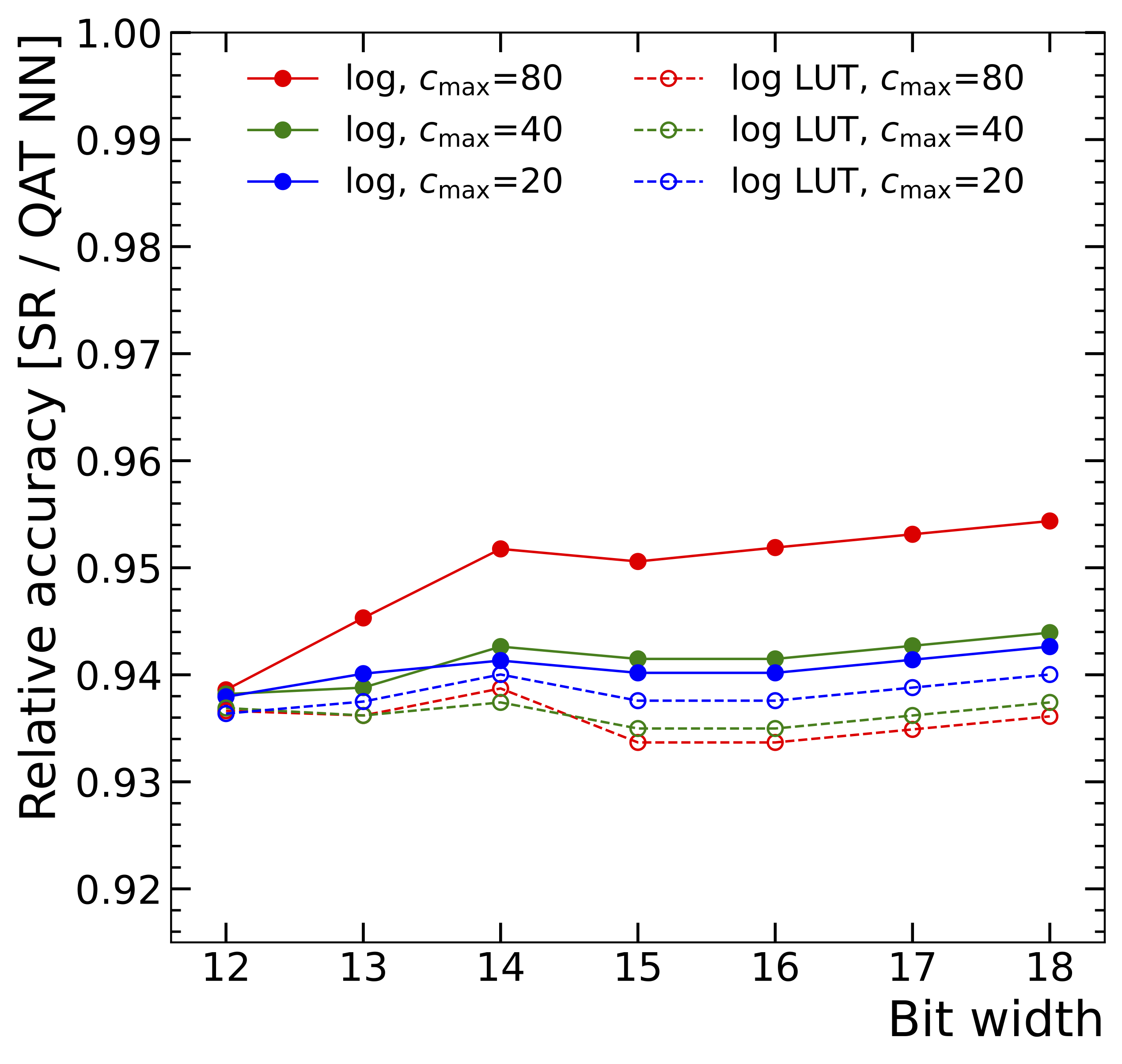
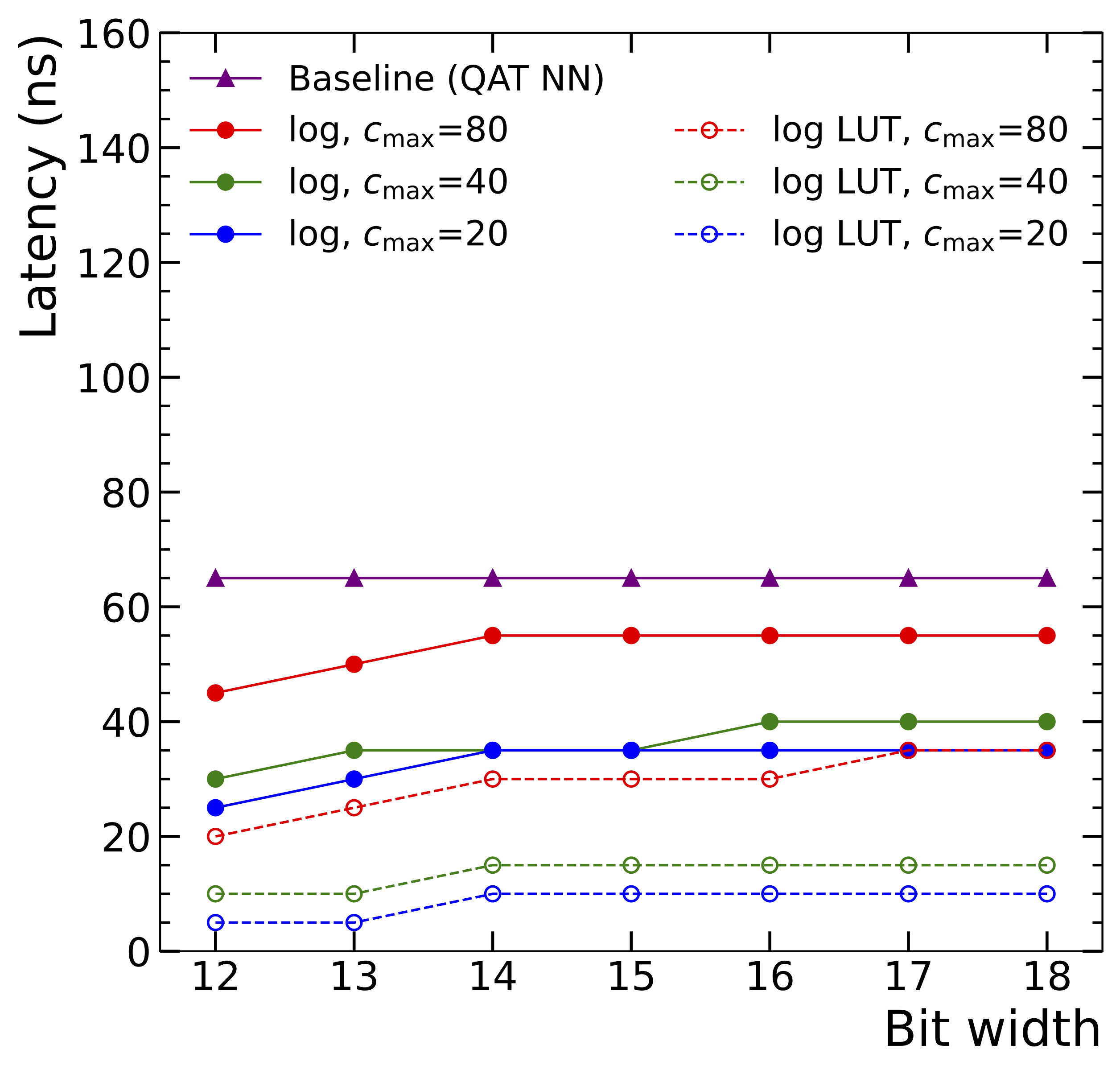
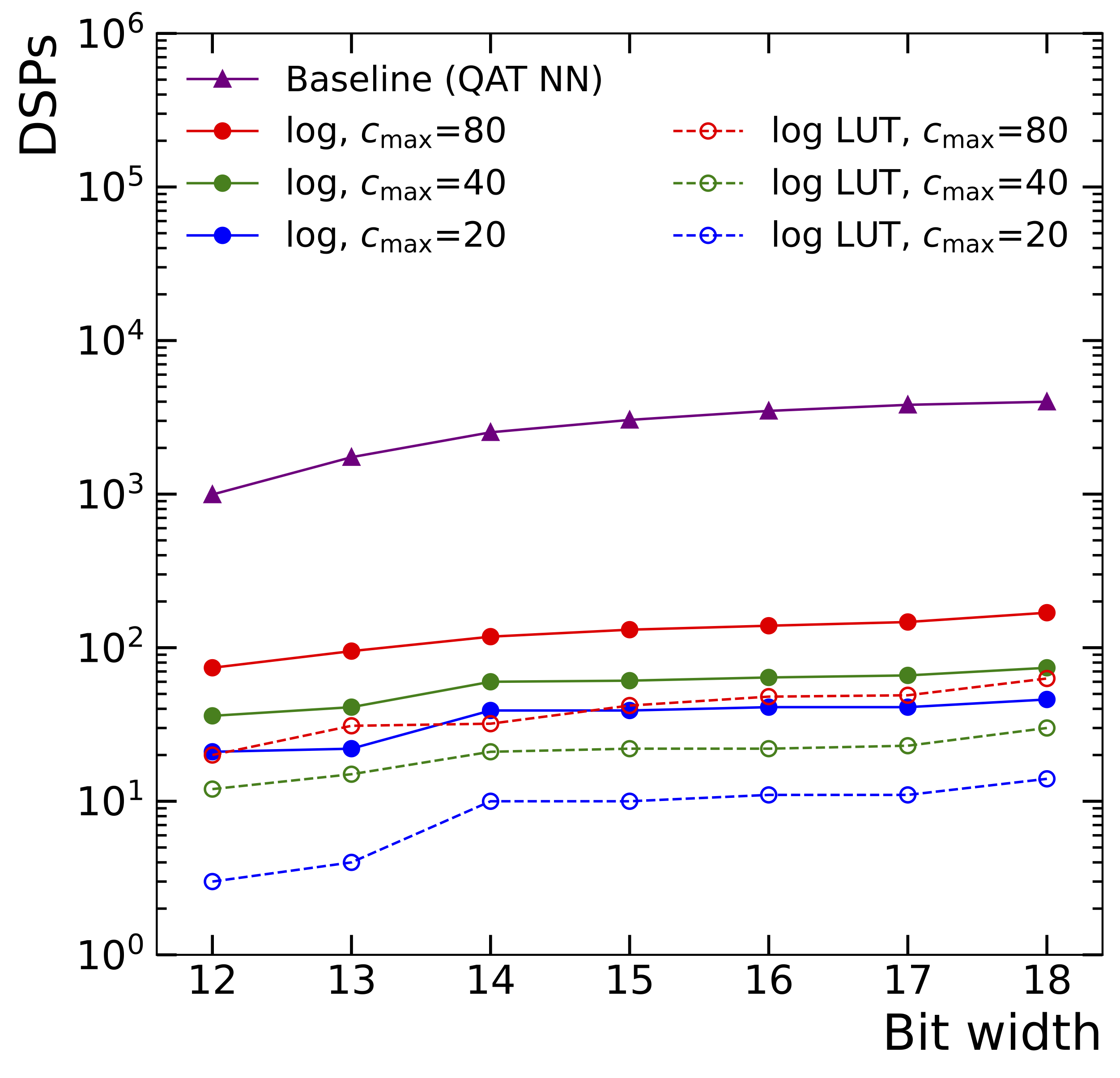
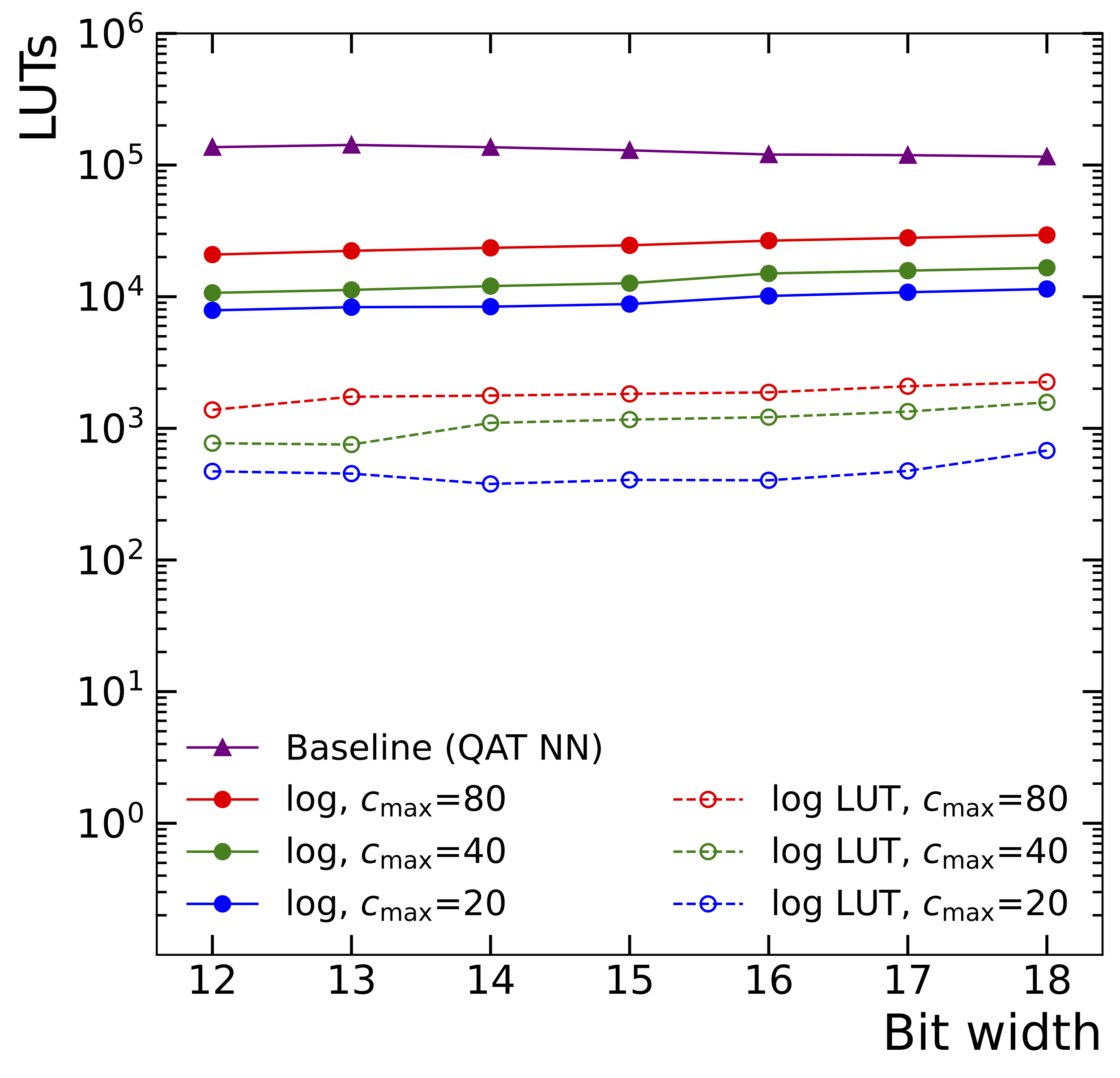
Symbolic Regression on FPGAs for Fast Machine Learning Inference
The high-energy physics community is investigating the potential of deploying machine-learning-based solutions on Field-Programmable Gate Arrays (FPGAs) to enhance physics sensitivity while still meeting data processing time constraints. In this contribution, we introduce a novel end-to-end procedure that utilizes a machine learning technique called symbolic regression (SR). It searches the equation space to discover algebraic relations approximating a dataset. We use pysr (a software to uncover these expressions based on an evolutionary algorithm) and extend the functionality of hls4ml (a package for machine learning inference in FPGAs) to support pysr-generated expressions for resource-constrained production environments. Deep learning models often optimize the top metric by pinning the network size because the vast hyperparameter space prevents an extensive search for neural architecture. Conversely, SR selects a set of models on the Pareto front, which allows for optimizing the performance-resource trade-off directly. By embedding symbolic forms, our implementation can dramatically reduce the computational resources needed to perform critical tasks. We validate our method on a physics benchmark: the multiclass classification of jets produced in simulated proton-proton collisions at the CERN Large Hadron Collider. We show that our approach can approximate a 3-layer neural network using an inference model that achieves up to a 13-fold decrease in execution time, down to 5 ns, while still preserving more than 90% approximation accuracy.
Paper: arXiv:2305.04099 Code: https://github.com/fastmachinelearning/hls4ml